WAVE
SCIENCE
Non-Breaking
Waves
Scientists
began to study waves in the late 18th and early 19th centuries.
They used a flow channel in which they could measure the speed,
height, and velocity of regular waves.
They found
that the wave speed and the wave length could be defined by a
simple formula:
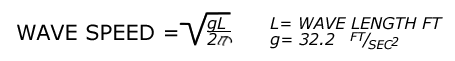
Thus a wave
with a wave length of 300 ft. will have a wave speed of 39 ft/sec.
(23 knots) and a period between wave crests of 7.7 seconds.
For regular
waves the wave height does not affect the wave speed.
These simple
relationships help us understand that waves are packets of energy
floating on the water surface. Each wave is similar to a pendulum.
The mass of waters moving up and down is the weight and the wave
length is similar to the length of the arm of the pendulum.
Note that
the weight of the water or the weight at the bottom of the pendulum
has no effect on the period of either a wave or a pendulum. In
fact the formula for the period of a simple pendulum is remarkably
similar to that of a wave.
Period of
a wave = A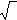 
L
seconds Period
of a pendulum = B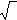
L seconds.
Where A and
B are constants and L is the wave length and pendulum arm length.
Thus waves
formed of liquid lead would have the same speed as water waves
A pendulum
would have the same period if the weight were lead or brass. Of
course this is why pendulums were used for clocks.
From these
studies we can obtain an effective engineering understanding of
regular waves. However, regular waves do not threaten a well found
yacht unless the yacht is permitted to surf down the forward face
and reach a high speed.
Return
to Top
Breaking
Waves
When
scientists increased the height of the waves in the flow channel
by moving the paddle more violently they observed that the waves
became very steep and collapsed forming a breaking wave. They
determined that the waves would break when the wave height exceeded
1/7 of the wave length.
Similarly
we know that a pendulum will cease to function if it swings up
too high.
A wave breaks
because its crest is too high for the forward speed of the wave.
The water cannot get over the crest, just as a yacht cannot get
over.
When a wave
breaks, water cascades down the forward face of the wave. Sailors
have described the face of a breaking wave as a waterfall. The
falling water makes a roaring sound, and from ancient times such
waves were known as "growlers".
Return
to Top
Worst Case
Breaking Wave Strike
I have chosen
the case of the Winston Churchill in the 1998 Sydney Hobart race
as an example of a worst case breaking wave. The Churchill was
a classic wooden sloop of 25 tons displacement and 55 ft. LOA.
Of the experienced crew of 9, two perished in the accident.
From "Fatal
Storm' by Mundle. "A sea came out of nowhere", said
Stanley, " I could feel it from where I was in the aft coach
house. It picked the boat up and rolled it down its face - 25
tons of boat- into the trough at a 45 degree angle. It was like
hitting a brick wall when we hit the bottom". A crewman below
reports that a sudden motion of the ship picked him up and threw
him 7 ft. He observed that 8 ft of the heavy timber bulwark and
planking had been torn off near the leeward shrouds, and the ribs
were exposed. . The boat filled rapidly and sank in a matter of
minutes.
This is an
unusual type of accident. Although there are records of many storm
casualties, I am aware of no documented instance of a well found
yacht of the size and reputation of the Churchill and crewed by
an ample group of expert sailors, suffering such catastrophic
structural damage that it sank in a matter of minutes. How could
this possibly happen? The severity or the storm was extreme but
by no means unprecedented. There are numerous reports of large
sailing yachts surviving hurricanes of the same general magnitude.
Although yachts have been lost in such storms I have been able
to find no record of comparable structural damage.
History shows
that the probability of a yacht being capsized and damaged by
a large breaking wave is strongly influenced by the displacement
of the vessel. Yachts under 35 ft. have a poor history while yachts
over 50 ft are rarely capsized and damaged.
The nature
and extent of the damage incurred by the Churchill is also most
unusual. The vessel was designed by Sparkman and Stevens and was
maintained to the highest standard. Yet the heavy timber bulwark
was shattered, the planking gone and the ribs exposed.
There is no
question of the fact that the leeward bow of the boat was driven
into solid green water at an extremely high velocity, far higher
than would be expected in a simple contact with a breaking wave.
We now have a technical understanding of how such a destructive
force can be generated. Observations from many experienced sailors
on a number of the SH yachts provide data which permit a sound
engineering analysis of the performance of the waves and the boats
in the race.
Water forces
are applied to the hull of a yacht by two means, buoyancy forces
and dynamic forces. Buoyancy forces are the familiar pressure
forces which keep the boat afloat. They never reach sufficient
magnitude to damage a well found yacht.
Dynamic forces
result from the motion of the boat relative to the water, either
as a result of the boat velocity or the water velocity due to
wave motion. A speeding power boat can be destroyed by striking
solid water. Similarly, a sailing yacht can be destroyed if it
is accelerated up to a high speed by a breaking wave strike and
then impacts solid green water in the preceding trough. This is
the fate that befell the Churchill.
To understand
this phenomenon we must consider the concept of energy. A moving
car or boat has energy. This form of energy is called kinetic
energy. Kinetic energy is measured in foot-pounds. Kinetic energy
can be calculated by the formula KE=1/2 (w/g) times (v²).
Where w is the weight of the car or boat, g is the acceleration
of gravity (32.2 ft/sec²) and v is the velocity in ft./sec.
Thus a 3,000
lb. weight traveling at 30 mph (44 ft./sec.) would have a kinetic
energy of 90,000 foot pounds. Now...and this is very important
to our understanding of the Churchill disaster...if the moving
vehicle strikes an object, the kinetic energy determines the severity
of the collision and the extent of the damage.
In addition
to energy due to motion, a vehicle can possess energy due to height.
This type of energy, also measured in foot pounds, is calculated
simply as the height times the weight. A 3000 lb car hoisted to
a height of 50 ft. would have 150,000 foot pounds of energy. If
dropped from 50 ft to a solid surface, the car would dissipate
this energy in damage. If the car was compressed by 2 ft. the
average force during the impact would be 75,000 pounds. If it
landed on its top and compressed four feet (because it was softer)
the average force would be 37,500 lbs. .These numbers (compression
and force) are not precise but the product must be the same to
satisfy the energy balance.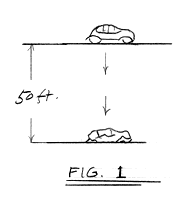
Since a car
accident is a more familiar event than a wave strike I will continue
with this analogy since it is technically identical to the Churchill
event.
Fig.1
shows a car being dropped from 50 ft. It will impact the ground
at 57 ft/sec (39 mph) and will have a collision energy of 150,000
ft. pounds. It will sustain the appropriate damage.
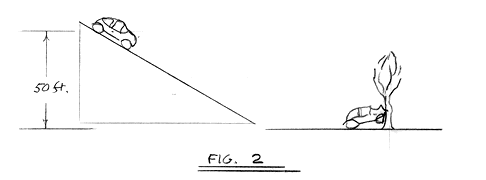
Fig. 2 shows the car on a ramp 50 ft. high. The car rolls
freely down the ramp and strikes a tree. The velocity at the bottom
of the ramp will be the same as if the car had been dropped vertically,
that is 57 ft/sec. Thus the collision damage will be comparable
to that of the vertical drop.
Now we come
to the key element in our study of storm damage. This explains
why the crew of the Churchill felt an impact similar to that of
striking another boat.
Fig. 3
Here we assume that the entire ramp is mounted on wheels and is
propelled toward the tree at 30 m.p.h. The moving ramp simulates
the front face of a large breaking storm wave. The car is released
from the top of the ramp and is permitted to roll down the face.
The " increase" in speed while descending the ramp is
the same as when the ramp is stationery, 39 m.p.h.. Thus the final
speed of the car as it leaves the ramp and strikes the tree is
30 plus 39 or 69 m.p.h..
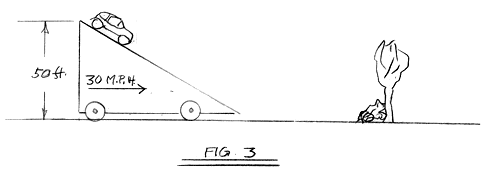
However since
the kinetic energy (collision energy) varies as the square of
the speed, the kinetic energy (collision energy} is 480,000 foot
lbs or over 3 times as much as if the ramp had been stationary.
There is no other wave - boat interaction which can generate such
destructive loads.
The wave in
this event acts as a sling shot, hurling the vehicle, car or boat
forward at a high velocity. This is the mechanism which destroyed
the Churchill and the same mechanical system that David used to
destroy Goliath.
With this
understanding we can design a simple system to decelerate the
boat before it strikes the solid water in the trough.
Return
to Top
An Experiment
The
sling shot concept can seem arcane. Actually it is simple.
It can be
accurately observed with no special equipment. All it takes is
a shovel with a curved blade and a golf ball.
Place the
golf ball in the center of a garage or cellar with a level floor.
Walk across the cellar at a constant (approximate) speed pushing the
shovel towards the ball. Adjust your walking speed such that the
ball is picked up and ascends up about 2/3 of the shovel height.
Maintain your
walking speed constant as the ball rolls down the blade and proceeds
to outrun the shovel. Except for friction effect, the ball will
leave the shovel at twice the speed at which you were walking.
When it strikes an object it will have 4 times the collision energy
of a ball moving at shovel speed.
